
- GSE Features
Deflection Calculations of Reinforced Concrete Slabs
TECHNICAL FEATURE // GSE CONCRETE SOFTWARE
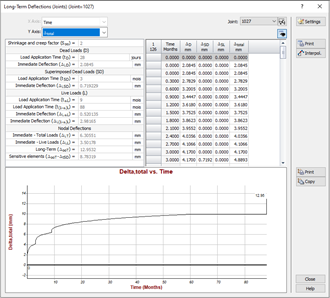
Hence, the cracked deflections calculation of concrete slabs has been developed. The cracking phenomenon increases the overall deflections of the slab. The service limit states ensure that the slab deflections do not exceed the given limit values to avoid causing serviceability problems.
The deflections of concrete slabs are composed of: immediate deflections and time-dependent deflections. The immediate deflections are calculated for the selected load combinations. The shrinkage and creep phenomenon are time-dependent effects causing deflections over long periods of time. The overall deflections of the building is a combination of both the immediate and time-dependent deflections.
The immediate cracked deflection calculations require an iterative analysis procedure where the loads are applied progressively. The initial finite element stiffness is calculated using the concrete isotropic elastic properties. As the loading intensity increases, the flexural efforts in the slabs also increase. Thus, cracks may form near high flexural effort areas. At those locations, the slab sectional inertias change and the concept of effective inertia Ie is used. The effective inertia is calculated according to the uncracked inertia Ig and the fully cracked inertia Icr. A well-known equation to calculate the effective inertia Ie is presented below:
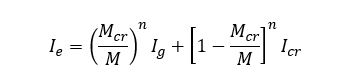
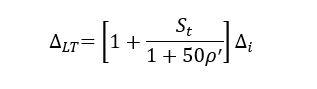
GSE Software
The GSE General Structural Engineering software is a fully integrated analysis and design software for structural engineering. The software accounts for steel, cold-formed steel, concrete, automated slab design, timber, light frame wood and aluminum.
EXPLORE THE GSE CONCRETE SOFTWARE
Related Posts

Variable anchorage slip in wood shearwalls
To enhance productivity of GSE Timber software’ users, the Anchorage Elongation Method can be defined as variable (tension only) and variable (tension and compression). The anchorage slip is calculated at each iteration according to the tension efforts at the anchorage locations.

Fatigue limit state
HSE users can efficiently set and edit all required fatigue parameters for the structure allowing to consider all applicable fatigue loads such as Galloping, Natural Wind Gust, or Truck-Induced Gust.

Live load reduction
The live load reduction is available for the GSE steel, concrete, aluminum, and wood modules. The live load reduction will be applied to the columns of the structure.
Live loads can be automatically reduced according to the selected method. The software computes the live load reduction factor (LLRF) that will reduce the effective axial compression force in columns.

Fire resistance of wood elements
The resistance limit states, under fire conditions, are calculated for large cross-section wood elements. To improve the productivity of GSE users, the elements cross-sections are automatically reduced during the limit state checks.


