
- Structural Analysis Features
Torsion and warping
TECHNICAL FEATURE // TORSION AND WARPING
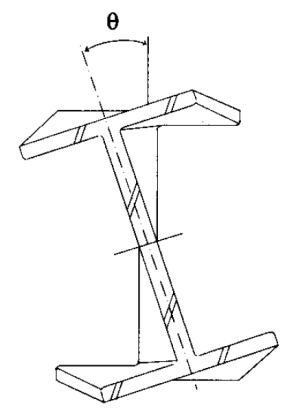
In addition to shear stresses, some members carry torque by axial stresses. This is called warping torsion. This happens when the cross-section wants to warp, i.e., displace axially, but is prevented from doing so during twisting of the beam. In other words, the section tends to resist torsion by out of plane bending of the flanges.
For solid and thin-wall closed sections (square, rectangular and circular tubes) these effects are often negligible. However, for thin-wall open sections restrained warping is often dominant. To include the effect of restrained warping we need to know the torsion constant J and the warping constant Cw which are geometric properties of the cross-section. For open shapes (I, C, Z, T, L, built-up …) the following equation may be used to evaluate the influence of the warping.
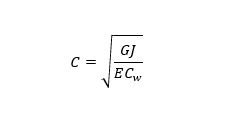
G Shear modulus of elasticity of the material
J Torsional constant for the cross section
E Modulus of elasticity of the material
Cw Warping constant for the cross-section
For axisymmetric cross-sections and thin-walled cross-sections with straight parts that intersect at one point such as X-shaped, T-shaped, and L-shaped cross-sections pure torsion will generally dominate over warping stresses. In these cases, torsional loads are carried by pure torsional shear stresses (St-Venant torsion) regardless of the boundary conditions.
Subscribe to our technical newsletter
Related Posts

IEEE PES Conference 2026
We’re thrilled to announce our participation as an exhibitor at the IEEE PES T&P Conference 2026, organized by the Power & Energy Society. Join us at Booth #3587 as we showcase the groundbreaking Virtual Tower Structures® (VTS) software.

NCSEA Structural Engineering Summit 2025
We’re excited to exhibit once again at the NCSEA Structural Engineering Summit! The 2025 edition will take place in New York City, and as returning participants, we’re proud to continue engaging with the community and showcasing tools that advance structural engineering! Join us at Booth #112.

Electrical Transmission and Substation Structures Conference 2025
We’re thrilled to announce our participation as an exhibitor at the Electrical Transmission & Substation Structures (ETS) Conference 2025, organized by the American Society of Civil Engineers ASCE! Join us at Booth #815 as we showcase the groundbreaking Virtual Tower Structures® (VTS) software.

NCSEA Structural Engineering Summit 2024
We’re thrilled to announce our participation as an exhibitor at the upcoming NCSEA 2024 Structural Engineering Summit. Join us at Booth #610.
